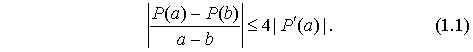Geometry and Analysis Seminar

 

Smale's mean value conjecture and the hyperbolic metric

Dr. T.W. Ng

The University of Hong Kong

Abstract

The following interesting result was proved by Steve Smale in 1981.

Theorem. Let P be a polynomial of degree d ?2 and a be any given complex number, then there exists some critical point b of P such that

Image25

Smale then asked whether one can replace the factor 4 in the upper bound in (1.1) by 1, or even possibly by (d - 1)/d. The conjecture has been verified for d = 2, 3, 4, and also in some other special circumstances but the general case remains open.

In this talk we shall show by using the method of hyperbolic metric that the constant 4 can be replaced by 4(d-2)/(d-1), where d is the degree of the polynomial. This first improvement of Smale's theorem is a joint work with Alan F. Beardon and David Minda.

Date:

November 1, 2000 (Wednesday)

Time:

4:00 - 5:00pm

Place:

Room 517, Meng Wah Complex

 

 

 

All are welcome