Extension of the Method
In general the number of hidden states can be more than two.
Suppose that the number of hidden states is m and the steady state probability distribution of the hidden
states is given by
a = (a1, a2,...,am)
Moreover, we let the number of observable state be n and when the hidden state is i (i = 1, 2, ... ,m),
the stationary distribution of the observable states is given by
(pi1, pi1, ... ,pin)
Here we assume that the model parameters m, n and pij are known.
Given an observed sequence of the observable states, one can of course calculate the occurrences of each state
in the sequence and hence the probability distribution q of the observable states.
Using the same trick as before, if we ignore the hidden states, the observable states follow the transition
probability matrix given by
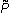 1= 1= |
é
ê
ê
ê
ë |
a1 |
a2 |
... |
am |
ù
ú
ú
ú
û |
| a1 |
a2 |
... |
am |
| : |
: |
: |
: |
| a1 |
a2 |
... |
am |
|
é
ê
ê
ê
ë |
p11 |
p12 |
... |
p1n |
ù
ú
ú
ú
û |
| p21 |
p22 |
... |
p2n |
| : |
: |
: |
: |
| pm1 |
pm2 |
... |
pmn |
|
= |
|
p |
where
| p= ( |
m
S
i=1 |
aipi1, |
m
S
i=1 |
aipi2, |
. . . |
m
S
i=1 |
aipin) |
It is easy to check that
p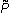 1=p and 1=p and |
n
S
i=1 |
pi = 1 |
Hence we have the following proposition.
Proposition 1 The vector p
is the steady state probability distribution of 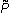 1. 1.
Therefore the transition probabilities of the hidden states
a = (a1, a2, . . . am)
can be obtained by solving
min
a |
||p-q|| subject to |
m
S
i=1 |
ai = 1 and a ³ 0. |
This is a standard constrained least square problem when ||.|| is chosen to be the
square of the L2-norm. We remark that when ||.|| is chosen to be the L1-norm,
the resulting optimization problem can be transformed into a linear programming problem, see for instance [2].
|